Pengertian dan Jenis-jenis Matriks
Nah, sudah disebutkan di awal nih, bahwa matriks adalah susunan bilangan-bilangan berbentuk persegi panjang yang diatur dalam baris atau kolom dengan dibatasi kurung. Bilangan yang tersusun dalam matriks disebut elemen/unsur matriks. Baris adalah susunan bilangan-bilangan yang mendatar (horizontal), sedangkan kolom adalah susunan bilangan-bilangan yang tegak (vertikal). Ordo matriks adalah banyaknya elemen baris dan banyaknya elemen kolom dari suatu matriks. Jika sebuah matriks memiliki i baris dan j kolom, maka matriks tersebut berordo i x j, dapat dituliskan Ai.j.
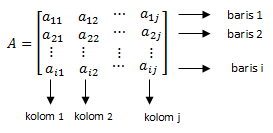
Jenis-jenis Vektor Matematika
Matriks terbagi menjadi beberapa jenis, diantaranya:
1. Matriks nol, matriks yang seluruh elemennya adalah bilangan nol.
2. Matriks baris, matriks yang hanya memiliki satu baris, berordo 1 x j.
3. Matriks kolom, matriks yang hanya memiliki satu kolom, berordo i x 1.
4. Matriks persegi, matriks yang banyaknya baris sama dengan banyaknya kolom, berordo i x i.
5. Matriks diagonal, matriks persegi yang semua elemennya nol, kecuali pada diagonal utamanya.
6. Matriks segitiga atas, matriks persegi yang semua elemen di bawah diagonal utamanya adalah nol.
7. Matriks segitiga bawah, matriks persegi yang semua elemen di atas diagonal utamanya adalah nol.
8. Matriks identitas, matriks persegi yang elemen pada diagonal utamanya adalah satu, sedangkan elemen lainnya adalah nol.

Dua matriks dikatakan sama (A=B) apabila mempunyai ordo yang sama dan elemen-elemen yang letaknya sama (bersesuaian) besarnya sama.
Operasi Matriks
Sobat Pintar tahu kan, kalau dua matriks dapat dioperasikan? Nah, Operasi matriks dapat dilakukan hanya jika memenuhi syarat dan ketentuannya. Operasi matriks sendiri meliputi : penjumlahan dan pengurangan dua matriks, perkalian matriks dengan bilangan skalar, perkalian dua matriks, dan transpose matriks.
Penjumlahan dan Pengurangan Matriks
Syarat penjumlahan dan pengurangan matriks yaitu : jika terdapat dua matriks, misal matriks A dan B, yang memiliki ordo sama, maka elemen-elemen yang seletak dapat dijumlahkan atau dikurangkan. Jumlah matriks A dan matriks B dapat dinyatakan dengan A+B, sedangkan selisih matriks A dan matriks B dapat dinyatakan dengan A – B.
Contoh :

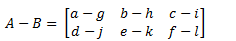
Perkalian Skalar pada Matriks
Pada operasi perkalian skalar, sebuah matriks dikalikan dengan bilangan skalar. Jika diketahui A merupakan suatu matriks dan K merupakan bilangan real, maka hasil perkalian K dengan matriks A adalah matriks yang diperoleh dengan mengalikan setiap elemen A dengan K.
Contoh :
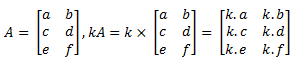
Perkalian Dua Matriks
Berbeda dengan perkalian skalar yang hanya mengalikan setiap elemen matriks dengan bilangan skalar, perkalian dua matriks memiliki aturan tersendiri. Syarat dua buah matriks, misal matriks A dan matriks B, dapat dikalikan adalah jika banyaknya kolom matriks A sama dengan banyaknya baris matriks B.
Bentuk perkalian antar matriks secara umum, yaitu :
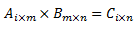
Untuk mencari hasil kali matriks A dengan matriks B ialah dengan mengalikan elemen pada baris-baris matriks A dengan elemen pada kolom-kolom matriks B, kemudian jumlahkan hasil perkalian antara baris dan kolom tersebut.
Contoh matriks :
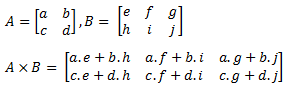
Transpose Matriks
Transpose suatu matriks, misal matriks A, yang dilambangkan dengan At adalah sebuah matriks yang disusun dengan cara menukarkan baris matriks A menjadi kolom matriks At dan kolom matriks A menjadi baris matriks At.
Contoh :
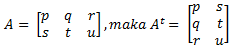
Determinan Matriks
Determinan suatu matriks didefinisikan sebagai selisih antara perkalian elemen-elemen pada diagonal utama dengan perkalian elemen-elemen pada diagonal sekunder. Determinan matriks hanya dapat ditentukan pada matriks persegi. Determinan dari matriks A dapat dituliskan det(A) atau |A|.
Untuk menentukan determinan dari sebuah matriks, terdapat dua aturan berdasarkan ordonya, yaitu ordo 2x2 dan ordo 3x3.
Contoh Soal Matriks

A. -196
B. -188
C. 21
D. 188
E. 196
Jawaban:
A. 196
Pembahasan:
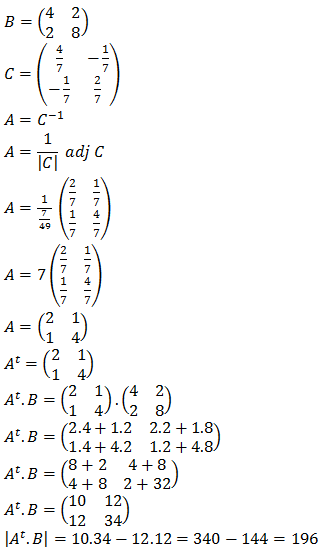
Daftar Pustaka

Tidak ada komentar:
Posting Komentar