Apa sih itu induksi matematika?
induksi matematika merupakan salah satu cara pembuktian rumus atau pernyataan matematika, atau lebih tepatnya metode pembuktian terhadap suatu pernyataan apakah pernyataan tersebut berlaku untuk setiap kasus. Supaya kebayang, sebaiknya kita langsung ke contoh kasus deh. Kasus yang seperti apa sih yang bisa diselesaikan dengan rumus induksi matematika? Kita masuk ke contoh yang sederhana aja deh ya. Misalkan saya punya deret bilangan seperti di bawah ini.
Langkah awal pembuktian untuk setiap n bilangan asli adalah nilai n tertentu, kita bisa mencari jumlah dari deret bilangan di atas. Sebagai contoh, untuk n=2, kita mendapatkan hasil demikian:
Ternyata untuk n=2, kita mendapatkan bahwa jumlah deretnya adalah 3.
Bagaimana dengan n=5? Gampang, tinggal kita hitung aja lagi begini:
Jumlahnya adalah 15. Kalau untuk n=8 gimana? Sama aja caranya:
l
Kita dapatkan bahwa untuk n=8, jumlah deret tersebut adalah 40.
Kemudian sudah mendapatkan informasi bahwa ternyata untuk menghitung jumlah deret tersebut untuk n bilangan asli berapapun, SUDAH ADA RUMUSNYA.
Konsep Dasar Induksi Matematika
Dengan menggunakan Induksi Matematika, kita bisa membuktikan rumus Sn di atas tanpa perlu menghitung satu per satu nilai Sn seperti di atas. Caranya simple banget. Kita cuma butuh melakukan dua langkah berikut ini:
Buktikan bahwa rumus tersebut benar untuk nilai ndasar (pada contoh di atas, buktikan untuk n=1).
Buktikan bahwa jika rumus tersebut benar untuk n=k, maka rumus tersebut juga benar untuk n=k+1.
Soal 1
Buktikanlah jika 32n + 22n + 2 benar-benar habis dibagi 5.
Agar bisa membuktikannya, maka sebaiknya Anda menerapkan beberapa tahapan diantaranya:
Langkah Pertama
32(1) + 22(1)+2 = 32 + 24 = 9 + 16 = 25, jadi benar-benar habis dibagi 5. Hal ini terbukti.
Langkah Kedua Menggunakan 2 (n = k)
32k + 22k + 2
Langkah Ketiga ( = k + 1)
= 32(k+1) + 22(2k+2)
= 32k+2 + 22k+2+2
= 32(32k) + 22(22k+2)
= 10(32k) + 5(22k+2) – 32k – 22k+2
= 10 (32k) + 5 (22k+2) – (32k + 22k+2)
Diperoleh:
10 (32k) sudah habis dibagi 5, 5(22k+2) sudah habis dibagi 5 dan –(32k) + 22k+2 juga habis dibagi 5.
Semua
Kemudian sudah mendapatkan informasi bahwa ternyata untuk menghitung jumlah deret tersebut untuk n bilangan asli berapapun, SUDAH ADA RUMUSNYA. Jadi, nggak perlu repot-repot menjumlahkan satu per satu seperti di atas, tapi tinggal kita masukkan saja nilai n ke dalam rumus tersebut. Bagaimana tuh rumusnya? Untuk deret di atas, rumus jumlahnya adalah demikian:
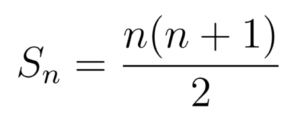
Wah, asik nih udah ada rumusnya. Berarti tinggal kita masukkin aja nilai n ke persamaan di atas untuk mencari jumlah deret tersebut. Nggak perlu jumlahin satu per satu. Nah, tapi sebagai matematikawan yang baik, kita harus skeptis nih, tahu dari mana bahwa rumus di atas itu benar? Tahu dari mana bahwa rumus tersebut berlaku untuk seluruh nilai n bilangan asli? Atau sederhananya,
Gimana Buktiinnya?
Yup. Gimana buktiinnya kalo rumus Sn di atas udah bener?
Nah, sebelum masuk ke pembuktian dengan Induksi Matematika, coba deh kita tes dulu apakah nilai Sn itu benar untuk nilai-nilai n yang sebelumnya udah kita hitung. Kita mulai dari n=2.
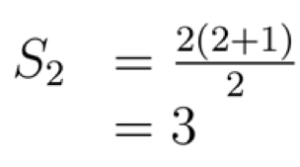
Wah, ternyata benar nih. Hasilnya sama untuk n=2. Sekarang coba kita tes untuk n=5.
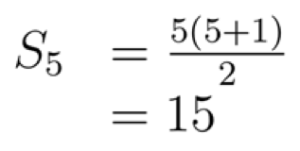
Hasilnya sama lagi nih. Untuk n=8 gimana?
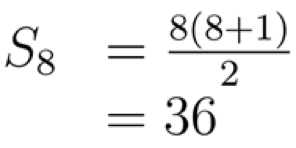
Bener lagi! Okay, kalau gitu, bisa kita simpulkan bahwa rumus Sn ini benar lah ya? Eit, tunggu dulu. Kita baru menguji untuk tiga nilai n. Dalam matematika, kita tidak bisa melakukan generalisasi seperti itu. Untuk bisa membuktikan bahwa rumus Sn ini benar untuk semua kasus, kita harus benar-benar bisa membuktikan bahwa rumus Sn ini benar untuk SEMUA nilai n bilangan asli.
Wah, kalau mau membuktikan untuk semua nilai n, kapan selesainya? Kan ada banyak banget yang harus dicoba. Nilai n=9, nilai n=10, nilai n=100, nilai n=84349384, dan seterusnya. Ada tak hingga nilai n yang harus kita coba. Nggak mungkin bisa kita cobain semuanya.
Nah, itulah sebabnya kita perlu membuktikannya dengan menggunakan Induksi Matematika.
Setelah elo baca penjabaran di atas, dapat disimpulkan bahwa ada tiga langkah dalam induksi matematika yang diperlukan untuk membuktikan sebuah rumus, yaitu:
- Membuktikan bahwa rumus atau pernyataan tersebut benar untuk n = 1.
- Mengasumsikan bahwa rumus atau pernyataan tersebut benar untuk n = k.
- Membuktikan bahwa rumus atau pernyataan tersebut benar untuk n = k + 1
Untuk menerapkan induksi matematika, kita harus bisa menyatakan pernyataan P (k + 1) ke dalam pernyataan P(k) yang diberikan. Untuk menyatakan persamaan P (k + 1), substitusikan kuantitas k + 1 ke dalam pernyataan P(k).
Sebelum lanjut, pastiin dulu elo udah punya aplikasi Zenius ya, biar bisa dapetin akses ke ribuan video pembelajaran dan latihan soal. Kalo belum install, langsung aja download dengan klik gambar di bawah ini!
Konsep Dasar Induksi Matematika
Dengan menggunakan Induksi Matematika, kita bisa membuktikan rumus Sn di atas tanpa perlu menghitung satu per satu nilai Sn seperti di atas. Caranya simple banget. Kita cuma butuh melakukan dua langkah berikut ini:
- Buktikan bahwa rumus tersebut benar untuk nilai n dasar (pada contoh di atas, buktikan untuk n=1).
- Buktikan bahwa jika rumus tersebut benar untuk n=k, maka rumus tersebut juga benar untuk n=k+1.
Okay, sampai di sini, kenapa dua langkah tersebut bisa membuktikan Sn benar untuk SEMUA nilai n bilangan asli?
karena efek domino.
Efek Domino
Elo pasti tau atau pernah maen domino kan? Yah, bahasa gaulnya gaple :p Emangnya apa nih hubungan antara domino atau gaple ini dengan induksi matematika? Coba kita lihat kedua langkah tersebut satu per satu ya. Mulai dari langkah pertama.
LANGKAH 1: Buktikan bahwa Sn benar untuk n=1.
Langkah pertama ini gampang banget. Tinggal kita masukkan nilai n=1 ke persamaan, terus kita hitung deretnya, beres. Kesimpulannya: S1 benar (Sn benar untuk n=1). Lanjut ke langkah 2.
LANGKAH 2: Buktikan bahwa jika benar untuk n=k, maka dia benar juga untuk n=k+1.
Ini bagian menariknya. Karena pada langkah pertama kita sudah membuktikan bahwa Sn benar untuk n=1, berarti dia benar juga untuk n=2. Kalau Sn benar untuk n=2, maka Sn benar juga untuk n=3. Kalau Sn benar untuk n=3, maka Sn benar juga untuk n=4. Dan seterusnya sampai n tak hingga.
Kalau penjelasan di atas masih kurang jelas, coba telaah pelan-pelan deh ya. Jadi bayangkan bahwa pembuktian yang kita lakukan di langkah 1 dan 2 tadi kita nyatakan dalam dua premis, premis 1 untuk pernyataan pada langkah 2 dan premis 2 untuk pernyataan pada langkah 1. Jadinya begini:
Premis 1: Jika Sn benar untuk n=k, maka Sn benar untuk n=k+1
Premis 2: Sn benar untuk n=1
Langkah-Langkah Mengerjakan Induksi Matematika
Induksi matematika sebetulnya merupakan semacam metode yang dipakai guna melakukan pemeriksaan terkait validasi pernyataan dalam himpunan bilangan positif maupun himpunan bilangan asli. Agar bisa melakukan pembuktian seperti ini, maka dibutuhkan dua langkah penting.
Langkah Basis
Langkah basis merupakan langkah awal untuk melakukan pembuktian induksi matematika. Langkah basis menunjukkan suatu pernyataan yang berlaku untuk bilangan 1.
Langkah Induksi
Setelah langkah basis, ada langkah induksi. Langkah induksi menunjukkan bahwa apabila pernyataan itu berlaku untuk suatu bilangan n = k, maka pernyataan tersebut juga berlaku bagi bilangan n = k + 1.
Prinsip Induksi Matematika
Ketika ingin mempelajari induksi matematika, maka sebaiknya cermati prinsip-prinsipnya terlebih dahulu. Setidaknya ada 4 prinsip yang harus dicermati saat membuktikan induksi matematika, diantaranya seperti berikut.
- Basis = tunjukkan p(1) adalah benar.
- Induksi = misalnya p(n) adalah benar untuk seluruh bilangan positif n = 1
- Langkah induksi memuat asumsi yang menyatakan tentang p (n) adalah benar. Asumsi ini disebut sebagai hipotesi induksi.
- Kesimpulan = pembuktian bahwa p (n+1) adalah benar.
Soal 1
Buktikanlah jika 32n + 22n + 2 benar-benar habis dibagi 5.
Agar bisa membuktikannya, maka sebaiknya Anda menerapkan beberapa tahapan diantaranya:
Langkah Pertama
32(1) + 22(1)+2 = 32 + 24 = 9 + 16 = 25, jadi benar-benar habis dibagi 5. Hal ini terbukti.
Langkah Kedua Menggunakan 2 (n = k)
32k + 22k + 2
Langkah Ketiga ( = k + 1)
= 32(k+1) + 22(2k+2)
= 32k+2 + 22k+2+2
= 32(32k) + 22(22k+2)
= 10(32k) + 5(22k+2) – 32k – 22k+2
= 10 (32k) + 5 (22k+2) – (32k + 22k+2)
Diperoleh:
10 (32k) sudah habis dibagi 5, 5(22k+2) sudah habis dibagi 5 dan –(32k) + 22k+2 juga habis dibagi 5.
Semua bilangan bulat tidak negatif n, buktikan dengan memakai induksi matematika bahwa 20 + 21 + 22 + … + 2n = 2n+1 – 1.
Cari tahu basis induksi terlebih dahulu yaitu 20 = 20+1 – 1. Jadi, sangat jelas bahwa 20 = 1
Jika p(n) benar, yakni 20 + 21 + 22 + … + 2n = 2n+1 – 1 adalah benar, maka tunjukkan bahwa p(n+1) juga benar: 20 + 21 + 22 + … + 2n = 2n+1 – 1 juga benar, maka tunjukkan bahwa 20 + 21 + 22 + … + 2n + 2n+1 = (20 + 21 + 22 + … + 2n) + 2n+1 = (2n+1 – 1) + 2n+1 (hipotesis induksi).
= (2n+1 + 2n+1) – 1
= (2.2n+1) – 1
= 2n+2 – 1
= 2(n+1)+1 – 1
Maka dapat dibuktikan bahwa semua bilangan bulat tidak negatif n, terbukti bahwa 20 + 21 + 22 + … + 2n = 2n+1 – 1.
Daftar pustaka
https://www.zenius.net/blog/induksi-matematika#Apa_sih_itu_induksi_matematika
https://mamikos.com/info/contoh-soal-induksi-matematika-pljr/

Tidak ada komentar:
Posting Komentar