Kelas: X IPS 1
Absen: 10
Sistem persamaan linear dan kuadrat atau disingkat SPLK adalah sistem persamaan yang terdiri atas sebuah persamaan linear dan sebuah persamaan kuadrat yang masing-masing bervariabel dua. Contoh SPLK adalah sebagai berikut.
y = 2 – x ………………. Persamaan (1)
y = x2 – 3x + 2 ……… Persamaan (2)
Contoh Soal:
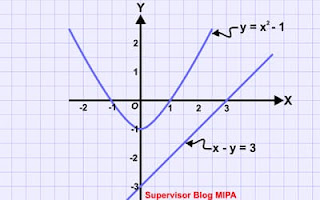
1. Carilah himpunan penyelesaian SPLK berikut, kemudian gambarkan sketsa tafsiran geometerinya.
y = x2 – 1
x – y = 3
Penyelesaian:
Persamaan x – y = 3 dapat kita tulis ulang menjadi bentuk berikut.
y = x – 3
subtitusikan y = x – 3 ke dalam persamaan y = x2 – 1 sehingga kita peroleh:
⇒ x – 3 = x2 – 1
⇒ x – 3 = x2 – 1
⇒ x2 – x – 1 + 3 = 0
⇒ x2 – x + 2 = 0
Persamaan kuadrat di atas sulit untuk difaktorkan. Jika kita hitung nilai diskriminannya dengan nilai a = 1, b = −1, dan c = 2, maka kita peroleh:
D = b2 – 4ac
D = (−1)2 – 4(1)(2)
D = 1 – 8
D = −7
Karena diskriminannya negatif (D < 1) maka persamaan kuadrat itu tidak memiliki penyelesaian. Oleh karena itu, SPLK di atas tidak memiliki penyelesaian sehingga himpunan penyelesaiannya dapat ditulis ∅. Interpretasi geometri dari SPLK ini adalah tidak adanya titik singgung maupun titik potong antara parabola dan garis lurus. Hal ini dapat kalian lihat pada gambar di bawah ini.
2. Carilah himpunan penyelesaian SPLK berikut, kemudian gambarkan sketsa tafsiran geometerinya.
x + y + 2
= 0
= 0
y = x2 – x – 2
Penyelesaian:
Persamaan x + y + 2 = 0 dapat kita tuliskan sebagai berikut.
y = −x – 2
Subtitusikan nilai y = −x – 2 ke persamaan y = x2 – x – 2 sehingga diperoleh:
⇒ −x – 2 = x2 – x – 2
⇒ x2 – x + x – 2 + 2 = 0
⇒ x2 = 0
⇒ x = 0
Subtitusikan nilai x = 0 ke persamaan y = −x – 2 sehingga diperoleh:
⇒ y = −(0) – 2
⇒ y = –2
Jadi, himpunan penyelesaiannya adalah {(0, −2)}. Tafsiran geometrinya berupa titik singgung antara garis lurus dan kurva parabola, yaitu di titik (0, −2) seperti yang ditunjukkan pada gambar berikut ini.
3. Carilah himpunan penyelesaian dari tiap sistem persamaan linear dan kuadrat (SPLK) berikut ini, kemudian buatlah grafik penyelesaiannya (sketsa tafsiran geometri).
a. y = x – 1 dan y = x2 – 3x + 2
b. y = x – 3 dan y = x2 – x – 2
c. y = −2x + 1 dan y = x2 – 4x + 3
Jawab:
a. Subtitusikan bagian linear y = x – 1 ke bagian kuadrat y = x2 – 3x + 2, sehingga diperoleh:
⇒ x – 1 = x2 – 3x + 2
⇒ x2 – 3x – x + 2 + 1 = 0
⇒ x2 – 4x + 3 = 0
⇒ (x – 1)(x – 3) = 0
⇒ x = 1 atau x = 3
Nilai x = 1 atau x = 3 disubtitusikan ke persamaan y = x – 1.
Untuk x = 1 diperoleh y = 1 – 1 = 0 → (1, 0)
Untuk x = 3 diperoleh y = 3 – 1 = 2 → (3, 2)
Jadi, himpunan penyelesaiannya adalah {(1,0), (3,2)}. Tafsiran geometrinya, garis y = x – 1 memotong parabola y = x2 – 3x + 2 di dua titik yang berlainan yaitu di (1, 0) dan di (3, 2). Perhatikan gambar di bawah ini.
b. Subtitusikan y = x – 3 ke y = x2 – x – 2 sehingga diperoleh:
⇒ x – 3 = x2 – x – 2
⇒ x2 – x – x – 2 + 3 = 0
⇒ x2 – 2x + 1 = 0
⇒ (x – 1)2 = 0
⇒ x = 1
Nilai x = 1 disubtitusikan ke persamaan y = x – 3 sehingga didapatkan
⇒ y = 1 – 3 = −2 → (1, −2)
Jadi, himpunan penyelesaiannya adalah {(1, −2)}. Tafsiran geometrinya, garis y = x – 3 menyinggung parabola y = x2 – x – 2 di titik (1, −2). Perhatikan gambar di bawah ini.
c. Subtitusikan y = −2x + 1 ke y = x2 – 4x + 3, diperoleh
⇒ −2x + 1 = x2 – 4x + 3
⇒ x2 – 4x + 2x + 3 – 1 = 0
⇒ x2 – 2x + 2 = 0
Persamaan kuadrat ini tidak mempunyai akar real, karena D = (−2)2 – 4(1)(2) = −4 < 0. Jadi, himpunan penyelesaiannya adalah himpunan kosong, ditulis ∅. Tafsiran geometrinya, garis y = −2x + 1 tidak memotong maupun menyinggung parabola y = x2 – 4x + 3. Perhatikan gambar berikut.
4. Carilah himpunan penyelesaian dari SPLK berikut ini.
x + y – 1 =
0 ……….bagian linear
0 ……….bagian linear
x2 + y2 – 25 = 0 …..bagian kuadrat berbentuk implisit yang tak dapat difaktorkan
Jawab:
Pada bagian persamaan linear, kita nyatakan y dalam x yaitu sebagai berikut.
⇒ x + y – 1 = 0
⇒ y = 1 – x
Lalu subtitusikan persamaan y = 1 – x ke persamaan kuadrat x2 + y2 – 25 = 0, sehingga kita peroleh:
⇒ x2 + y2 – 25 = 0
⇒ x2 + (1 – x)2 – 25 = 0
⇒ x2 + 1 – 2x + x2 – 25 = 0
⇒ 2x2 – 2x – 24 = 0
⇒ x2 – x – 12 = 0
⇒ (x + 3)(x – 4) = 0
⇒ x = −3 atau x = 4
Setelah nilai-nilai x kita peroleh, selanjutnya subtitusikan x = −3 atau x = 4 ke persamaan linear x + y – 1 = 0 yaitu sebagai berikut.
● untuk x = −3 diperoleh:
⇒ x + y – 1 = 0
⇒ −3 + y – 1 = 0
⇒ y – 4 = 0
⇒ y = 4
Kita peroleh himpunan penyelesaian (−3, 4).
● untuk x = 4 diperoleh:
⇒ x + y – 1 = 0
⇒ 4 + y – 1 = 0
⇒ y + 3 = −3
⇒ y = 4
Kita peroleh himpunan penyelesaian (4, −3).
Jadi, himpunan penyelesaiannya adalah {(−3, 4), (4, −3)}. Anggota-anggota dari himpunan penyelesaian SPLK tersebut dapat ditafsirkan sebagai koordinat titik potong garis x + y = 1 dengan lingkaran x2 + y2 = 25. Perhatikan gambar berikut ini.
5. Carilah himpunan penyelesaian dari SPLK berikut ini.
2x + 3y = 8
4x2 – 12xy + 9y2 = 16
Jawab:
Bagian kuadrat dapat difaktorkan sebagai berikut.
⇒ 4x2 – 12xy + 9y2 = 16
⇒ (2x – 3y)2 – 16 = 0
⇒ (2x – 3y + 4)(2x – 3y – 4) = 0
⇒ 2x – 3y + 4 = 0 atau 2x – 3y – 4 = 0
Jika hasil ini digabungkan dengan persamaan linear semula, maka akan diperoleh dua SPLDV, yaitu sebagai berikut.






Tidak ada komentar:
Posting Komentar