Nama: Eva Awalia Safitri Harahap
Kelas: X IPS 1
Absen: 10
SISTEM PERTIDAKSAMAAN KUADRAT DAN KUADRAT
Sistem pertidaksamaan kuadrat dua variabel terdiri dari dua pertidaksamaan kuadrat. Salah satu metoda yang paling populer dalam menyelesaikannya adalah dengan metoda grafik. Langkah-langkah penyelesaian dengan metoda ini adalah sebagai berikut:
1. Anggap kedua pertidaksamaan kuadrat tersebut sebagai fungsi kuadrat, dan gambarkan grafik-grafiknya dalam tata koordinat Cartesius.
2. Gunakan titik-titik uji untuk menentukan daerah penyelesaian dari masing-masing pertidaksamaan, lalu kemudian arsirlah daerah penyelesaian masing-masing pertidaksamaan tersebut dengan warna atau arah garis yang berbeda-beda.
3. Daerah penyelesaian sistem pertidaksamaan adalah irisan kedua daerah pertidaksamaan itu.
CONTOH SOAL:
01. Gambarlah kedua pertidaksamaan kuadrat berikut ini dalam satu sistem koordinat Cartesius, kemudian tentukan daerah penyelesaiannyay > x2 – 9
y ≤ –x2 + 6x – 8
Jawab
a. Gambar daerah penyelesaian pertidaksamaan y > x2 – 9(1) Tititk potong dengan sumbu-X syarat y = 0
x2 – 9 = 0
(x + 3)(x – 3) = 0
x = –3 dan x = 3
Titik potongnya (–3, 0) dan (3, 0)
(2) Tititk potong dengan sumbu-Y syarat x = 0
y = x2 – 9
y = (0)2 – 9
y = –9
Titik potongnya (0, –9)
(3) Menentukan titik minimum fungsi y = x2 – 9
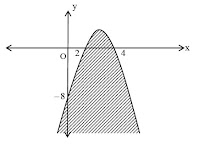
(4) Gambar daerah penyelesaiannya
(Daerah yang diarsir adalah daerah penyelesaian)
b. Gambar daerah penyelesaian pertidaksamaan y ≤ –x2 + 6x – 8
(1) Tititk potong dengan sumbu-X syarat y = 0
–x2 + 6x – 8 = 0
x2 – 6x + 8 = 0
(x – 4)(x – 2) = 0
x = 4 dan x = 2
Titik potongnya (4, 0) dan (2, 0)
(2) Tititk potong dengan sumbu-Y syarat x = 0
y = –x2 + 6x – 8
y = –(0)2 + 6(0) – 8
y = –8
Titik potongnya (0, –8)
(3) Menentukan titik maksimum fungsi y = –x2 + 6x – 8
(4) Gambar daerah penyelesaiannya
(Daerah yang diarsir adalah daerah penyelesaian)
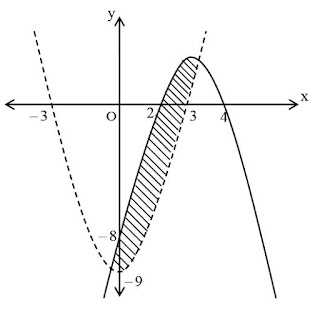
Daerah penyelesaian kedua pertidaksamaan itu adalah irisan dua daerah penyelesaian masing-masing pertidaksamaannya, yakni:
Sistem pertidaksamaan kuadrat dua variabel terdiri dari dua pertidaksamaan kuadrat. Salah satu metoda yang paling populer dalam menyelesaikannya adalah dengan metoda grafik. Langkah-langkah penyelesaian dengan metoda ini adalah sebagai berikut:
1. Anggap kedua pertidaksamaan kuadrat tersebut sebagai fungsi kuadrat, dan gambarkan grafik-grafiknya dalam tata koordinat Cartesius.
2. Gunakan titik-titik uji untuk menentukan daerah penyelesaian dari masing-masing pertidaksamaan, lalu kemudian arsirlah daerah penyelesaian masing-masing pertidaksamaan tersebut dengan warna atau arah garis yang berbeda-beda.
3. Daerah penyelesaian sistem pertidaksamaan adalah irisan kedua daerah pertidaksamaan itu.
1. Anggap kedua pertidaksamaan kuadrat tersebut sebagai fungsi kuadrat, dan gambarkan grafik-grafiknya dalam tata koordinat Cartesius.
2. Gunakan titik-titik uji untuk menentukan daerah penyelesaian dari masing-masing pertidaksamaan, lalu kemudian arsirlah daerah penyelesaian masing-masing pertidaksamaan tersebut dengan warna atau arah garis yang berbeda-beda.
3. Daerah penyelesaian sistem pertidaksamaan adalah irisan kedua daerah pertidaksamaan itu.
CONTOH SOAL:
01. Gambarlah kedua pertidaksamaan kuadrat berikut ini dalam satu sistem koordinat Cartesius, kemudian tentukan daerah penyelesaiannya
y > x2 – 9
y ≤ –x2 + 6x – 8
Jawab
a. Gambar daerah penyelesaian pertidaksamaan y > x2 – 9
y ≤ –x2 + 6x – 8
Jawab
a. Gambar daerah penyelesaian pertidaksamaan y > x2 – 9
(1) Tititk potong dengan sumbu-X syarat y = 0
x2 – 9 = 0
(x + 3)(x – 3) = 0
x = –3 dan x = 3
Titik potongnya (–3, 0) dan (3, 0)
x2 – 9 = 0
(x + 3)(x – 3) = 0
x = –3 dan x = 3
Titik potongnya (–3, 0) dan (3, 0)
(2) Tititk potong dengan sumbu-Y syarat x = 0
y = x2 – 9
y = (0)2 – 9
y = –9
Titik potongnya (0, –9)
(3) Menentukan titik minimum fungsi y = x2 – 9
(4) Gambar daerah penyelesaiannya
(Daerah yang diarsir adalah daerah penyelesaian)
(Daerah yang diarsir adalah daerah penyelesaian)
b. Gambar daerah penyelesaian pertidaksamaan y ≤ –x2 + 6x – 8
(1) Tititk potong dengan sumbu-X syarat y = 0
–x2 + 6x – 8 = 0
x2 – 6x + 8 = 0
(x – 4)(x – 2) = 0
x = 4 dan x = 2
Titik potongnya (4, 0) dan (2, 0)
(2) Tititk potong dengan sumbu-Y syarat x = 0
y = –x2 + 6x – 8
y = –(0)2 + 6(0) – 8
y = –8
Titik potongnya (0, –8)
(1) Tititk potong dengan sumbu-X syarat y = 0
–x2 + 6x – 8 = 0
x2 – 6x + 8 = 0
(x – 4)(x – 2) = 0
x = 4 dan x = 2
Titik potongnya (4, 0) dan (2, 0)
(2) Tititk potong dengan sumbu-Y syarat x = 0
y = –x2 + 6x – 8
y = –(0)2 + 6(0) – 8
y = –8
Titik potongnya (0, –8)
(3) Menentukan titik maksimum fungsi y = –x2 + 6x – 8
(4) Gambar daerah penyelesaiannya
(Daerah yang diarsir adalah daerah penyelesaian)
(Daerah yang diarsir adalah daerah penyelesaian)
Daerah penyelesaian kedua pertidaksamaan itu adalah irisan dua daerah penyelesaian masing-masing pertidaksamaannya, yakni:
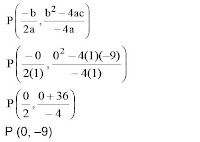



Tidak ada komentar:
Posting Komentar